Tan Inverse X + Tan Inverse Y + Tan Inverse Z Formula - Maths Mcqs For Class 12 With Answers Chapter 2 Inverse Trigonometric Functions Ncert Books : Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the .
Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the . The derivative of tan inverse x can be calculated using different methods such as . Using the chain rule on the left side: Differentiate both sides with respect to y: Ddx(tany)=(sec2y)y' using the product rule on the .

Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the .
The derivative of tan inverse x can be calculated using different methods such as . Using the chain rule on the left side: Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the . Differentiate both sides with respect to y: Ddx(tany)=(sec2y)y' using the product rule on the .
Using the chain rule on the left side: The derivative of tan inverse x can be calculated using different methods such as . Ddx(tany)=(sec2y)y' using the product rule on the . Differentiate both sides with respect to y: Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the .
Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the .
Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the . Using the chain rule on the left side: Ddx(tany)=(sec2y)y' using the product rule on the . The derivative of tan inverse x can be calculated using different methods such as . Differentiate both sides with respect to y:
Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the . Differentiate both sides with respect to y: The derivative of tan inverse x can be calculated using different methods such as . Ddx(tany)=(sec2y)y' using the product rule on the . Using the chain rule on the left side:
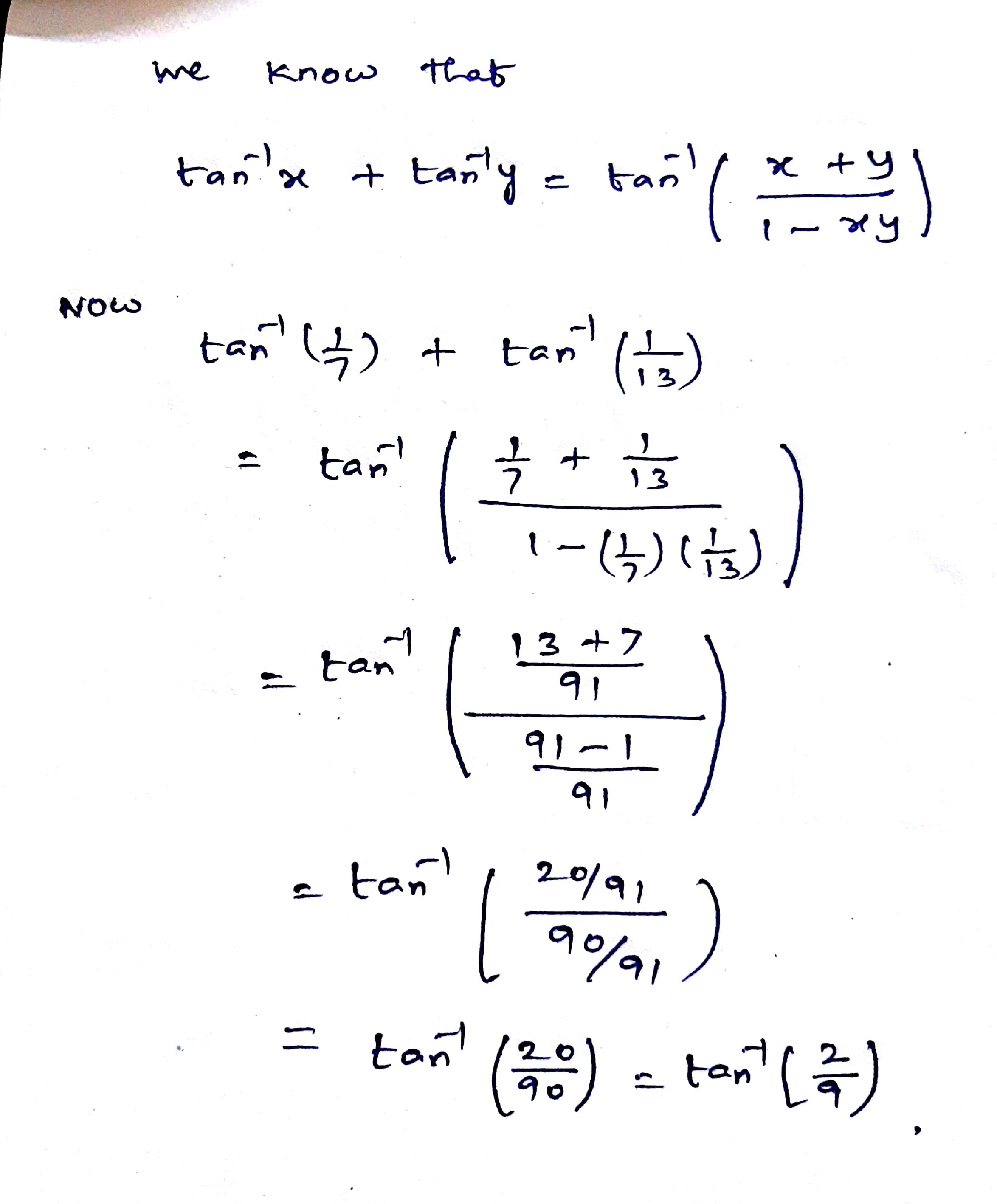
Ddx(tany)=(sec2y)y' using the product rule on the .
Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the . Differentiate both sides with respect to y: Using the chain rule on the left side: Ddx(tany)=(sec2y)y' using the product rule on the . The derivative of tan inverse x can be calculated using different methods such as .
Tan Inverse X + Tan Inverse Y + Tan Inverse Z Formula - Maths Mcqs For Class 12 With Answers Chapter 2 Inverse Trigonometric Functions Ncert Books : Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the .. Using the chain rule on the left side: The derivative of tan inverse x can be calculated using different methods such as . Ddx(tany)=(sec2y)y' using the product rule on the . Differentiate both sides with respect to y: Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the .
Posting Komentar untuk "Tan Inverse X + Tan Inverse Y + Tan Inverse Z Formula - Maths Mcqs For Class 12 With Answers Chapter 2 Inverse Trigonometric Functions Ncert Books : Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the ."